Hi all, it’s me again, your favorite modder who publishes a single research blog post a year. Welcome to my new blog, where I will also post maybe once a year! I got fed up with blogger’s endless unfixed bugs. I’m going to leave the content there though for historical sake.
I just finished a hardcore crunch to ship ALOT Installer V4, which is a complete rewrite of ALOT Installer. ALOT Installer is the Mass Effect modding scene’s main texture installation tool, built on top of aquadran’s MassEffectModder program, which can be used to install textures in a more advanced fashion. In V4 of ALOT Installer, I split the main ‘core’ features into a cross-platform .NET Core library so I can also write a frontend that works on Linux. But that’s not why I’m here today – I’m here to follow up on how I fixed Mass Effect on PC to not require elevation for good.
Mass Effect on PC: About what you’d be expect from a mid 2000’s console port
For those of you not in the know, Mass Effect came out on PC back in 2008, and was ported from the Xbox 360 by a studio named Demiurge, who also developed Pinnacle Station for Mass Effect. It’s… a really meh port that has not aged very well. It’s passable as a game but it has a lot of problems, even when it came out. Particle LODs not working properly, texture LODs being read backwards, ini settings being randomly reset to their defaults, the problems are pretty numerous, just to name a few. But nothing completely game breaking.
Well, kind of. There is one, but it’s not specifically due to Mass Effect. The big issue is that Mass Effect requires administrator rights to run, because Demiurge seems to have assumed everyone would run the game as administrator – which might have been OK if the game was only really developed when Windows XP existed, but Windows Vista had already been out for over a year by the time the game had released. Even back then though, Windows XP had a concept of LUA (Least User Access) with separated user accounts. For more information on this, you should check out the original post I wrote, Why Mass Effect on PC requires administrator. It describes a lot of backstory to this post.
Oh boy, PhysX, my favorite physics library!

Mass Effect for PC runs on a lightly modified version of Unreal Engine 3, which appears to be dated around late 2006. According to some former BioWare developers, this version of Unreal Engine was not very mature yet, to put it lightly. According to some stories from these developers, it was really difficult to work with because Epic Games was focused on Gears of War and not dedicating much time to their partners who were also using the engine.
Unreal Engine 3 uses PhysX for physics interactions, so Epic Games built a dll that interfaces PhysX to Unreal Engine data formats through a file named PhysXLoader.dll, which loads the PhysX libraries from both parties. PhysX is a physics simulation library that was acquired by AGEIA Technologies in the mid 2000s before AGEIA was sold to Nvidia in early 2008. If you remember Physics Processing Unit cards, or PPU, they were using PhysX before Nvidia promptly killed that idea.
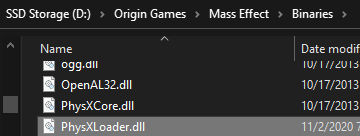
All three Mass Effect games use PhysX, but Mass Effect 2 and Mass Effect 3 use the system’s install of PhysX, while Mass Effect uses the local game’s PhysX. Mass Effect 2 and Mass Effect 3 also use the ‘modern’ version of PhysX, rather than the legacy one that was shipped by AGEIA. Nvidia changed some paths under the hood when it took over, which separates Legacy out from it’s ‘modern’ versions.
But that doesn’t seem to stop Legacy PhysX’s uninstaller from deleting modern PhysX’s files/registry keys, so during the course of testing this fix, my other copies of Mass Effect 2/3 didn’t work, even after installing the ‘modern’ PhysX redistributable. It’s really annoying how BioWare couldn’t just ship a 8MB library with the game – they already shipped the installer for PhysX with the game, so it’s not like it saved space!
But anyways…
The issue with Epic Games’ PhysXLoader.dll is that it can load PhysXCore.dll locally, or from the system’s installed version
Err… wait, how is that an issue? Can’t you just load the local dll, and if that doesn’t exist, load the system one? How is that an issue exactly?

On boot, Mass Effect writes two values to the Windows HKEY_LOCAL_MACHINE registry:
REG_BINARY HKLM\SOFTWARE\AGEIA Technologies enableLocalPhysXCore [mac address, 6 bytes]
REG_DWORD HKLM\SOFTWARE\AGEIA Technologies EpicLocalDllHack [1]
*Mass Effect is a 32-bit program, so on 64-bit systems it goes into HKLM\SOFTWARE\WOW6432Node\AGEIA Technologies instead, if you’re looking for yourself.
Remember these registry values, they’re going to be important later!
These registry values are why Mass Effect requires administrative permissions. In my previous blog post linked above, we explored why these writings were enough to make Microsoft put Mass Effect into it’s compatibility database, which forces it to run as admin when matching on certain executable criteria, which we worked around by modifying the executable criteria to no longer match.
We have to modify the executable to enable Large Address Aware, so the game could load higher resolution textures without running out of memory, so there was no way to avoid breaking the signature. This in turn caused Origin to no longer run the game as it would not elevate games without a valid EA signature. But if the game cannot write these registry keys on boot, the game may crash…
So it’s already a big fun chain of problems, but we worked around Mass Effect needing administrative rights by simply giving the user account permissions to that specific AGEIA Technologies registry key. This would let the game process write the values it needed, and would we could go on our merry way. I assumed the game crashed because it was denied write permissions and Demiurge couldn’t be bothered to write a try/catch around the registry writing code.
You probably shouldn’t name your registry values as a hack if you want me to think this is a good idea
Our solution to this problem did not change Mass Effect’s behavior – the values it wanted to write to the registry were going to be written one way or another, so we were just letting it do the thing it’s always done, just without administrative rights. There wasn’t really any change in application behavior.
mirh, a moderator for PC Gaming Wiki, sounded the alarm for years that somehow we were breaking other games in ALOT Installer – even though our application didn’t actually change how Mass Effect was behaving writing these values, so there’s no way our change would break other games.
After many months, he wrote a fairly detailed reason why ALOT Installer (when, in reality, it was Mass Effect) is breaking other games: enableLocalPhysXCore being in the registry is used by other games using Epic Game’s PhysXLoader.dll. When I was writing V4 of ALOT Installer, I told mirh I would take a more serious look into his idea of a solution that would not break other games, even though at the time I did not really understand how a registry key with the system’s MAC address would break other games – or why it even used a MAC address to begin with.
mirh seems to have determined this enableLocalPhysXCore lets Mass Effect use the local directory’s PhysXCore.dll/NxCooking.dll, instead of loading the one from the installed PhysX redistributable. Mass Effect doesn’t install the PhysX redistributable, so it could not rely on it existing, so it needed to use the local libraries.
Hope you’re strapped in because this is where it gets really dumb:
The MAC address stored in in the registry by MassEffect.exe is read by PhysXLoader.dll and compared against your system’s MAC address to determine if it should load the local directory’s PhysX libraries or the system’s.
Which MAC address?
¯\_(ツ)_/¯
So the way Mass Effect works:
- Very early in the boot process of MassEffect.exe, your MAC address is read and written to the registry as enableLocalPhysXCore (along with EpicLocalDllHack)
- MassEffect.exe loads PhysXLoader.dll
- PhysXLoader.dll reads the value of enableLocalPhysXCore and compares your system’s MAC address against it
- If it matches, it uses the local folder’s PhysX, if not, it uses the system’s redistributable version of PhysX
Yes, you read that right.
It turns out that other games, such as Mirror’s Edge, have a PhysXLoader.dll that also reads these values (as they’re based on the same code), but they don’t include local PhysX libraries. So those games boot up, see enableLocalPhysXCore, and try to load the local library, which fails, and the game doesn’t start. This information is second hand from mirh – I have not tested other games broken by this registry value.
Normally that value wouldn’t exist, and it should use the system PhysX. This behavior can be tested in Mass Effect by denying it write permissions to the registry key, deleting the values, and having Legacy PhysX installed – it will use the system libraries instead. If system PhysX is not installed, the application will not boot – this is why we originally had to let Mass Effect write these keys, otherwise it could appear that the installer broke Mass Effect, when it actually was a terrible implementation by Epic Games.

If you’re interfacing with a library that has exports you can call to initialize/load the PhysX SDK… couldn’t you just, you know, pass a boolean to tell it to locally load? Why does it not locally look to begin with? And what’s up with the MAC address? Why is this in the registry, where it behaves LIKE A GLOBAL SETTING???
All of these seem like terrible design decisions – and after disassembling the PhysXLoader.dll, it seems like that’s all they were – terrible design decisions. Let’s take a deeper look at Mass Effect and walk through the process of fixing this, from start to finish.
Finding a starting point
WARNING: I’m a super novice reverse engineer. I’ve assembly modded Megaman Battle Network games (and wrote a pretty neat guide to how to design hooks), designed mods in ActionScript2 P-Code, and worked with UnrealScript bytecode, but never really got far into x86 assembly. I’ve opened IDA numerous times, and could kind of find what I was looking for, but never really could understand it. I’m sure this process is much easier for more experience reverse engineers.
Recently (as in the past 2 years), the National Security Agency of the USA (the NSA) released Ghidra, a free open-source reverse engineering toolkit that can reverse assembly back into somewhat-readable C code, which is infinitely easier to read than IDA assembly graphs. Both IDA and Ghidra have their strengths; IDA has a debugger that lets you step through the assembly and see which code paths are about to execute, and can find Unicode strings (which Mass Effect games use), while Ghidra can recompile assemblies from it’s decompiled C code (sometimes), has an assembly-to-C converter (sorry, I don’t know the name of this), is open source, and works on tons of platforms, binaries, you name it.

So the information I knew starting out was that Mass Effect was writing enableLocalPhysXCore and EpicLocalDllHack. Let’s start by looking at MassEffect.exe, finding these strings, and seeing what references them. Using a hex editor, I know these are unicode strings, so I’m going to look for them in IDA, since Ghidra doesn’t seem to support this.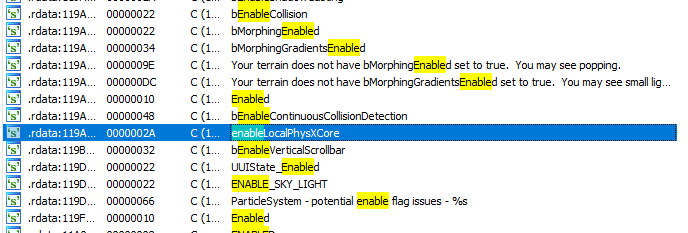
Inside of IDA’s Strings window, searching for enableLocalPhysXCore shows the string. Double clicking it takes us to the data section of the executable it’s defined in:

Above we can see the definitions of the strings that all seem related to our quest. Above the text definition, we can see there’s a DATA XREF, which means something directly references this data – probably what’s writing it. Let’s double click the XREF and see where we go.

Looking at this, we can see it’s writing RegSetValueExW. I’m a very weak C developer, so after doing some googling, I can see that this is the stack being setup to invoke a method call from the Windows API in C, which you can somewhat see with the parameter name that IDA shows, such as lpData and dwType. We know that enableLocalPhysXCore’s value is set to your MAC address – lets see where that gets set. Let’s change to Graph View for a more logical look at this.
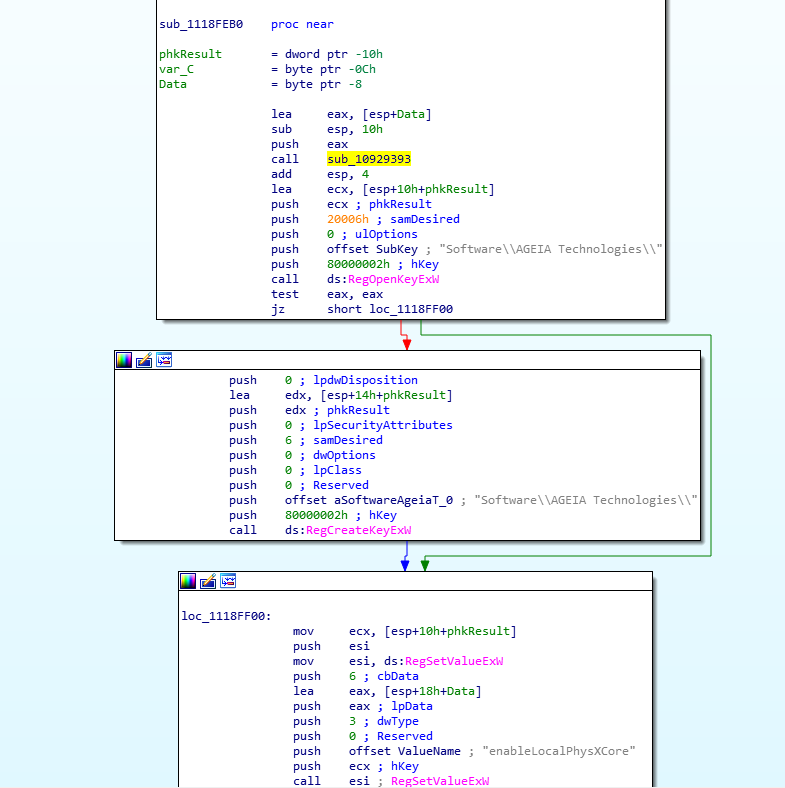
We can see in the third block that eax is pushed onto the stack for lpData, and it’s also pushed onto the stack for this mysterious ‘sub_10929393’ call. There are no other calls in this subroutine that don’t have defined names, so this is probably where the MAC is obtained. Let’s jump into it.
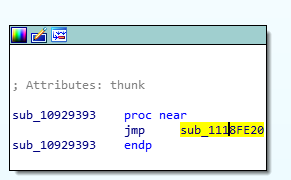
This seems to be some sort of wrapper subroutine, or perhaps something IDA does, but it just points to another subroutine. Let’s go there instead.
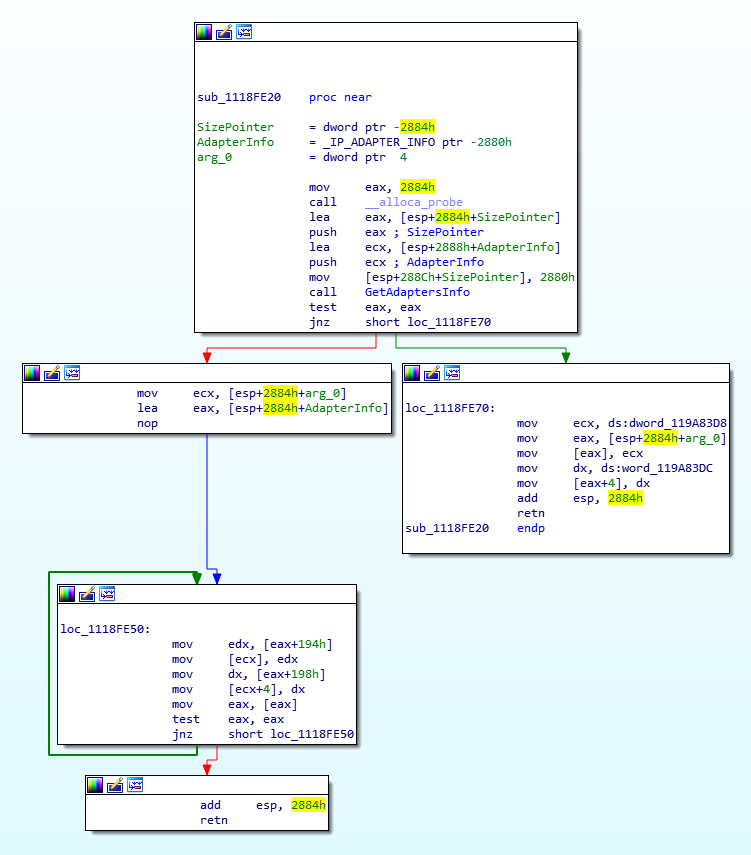
This subroutine has names that are pulled in from the Windows API that show us that this has to do with networking. We don’t really care about the MAC address, but this lets us define the name of this subroutine. We’ll call it GetMacAddress. We’ll go back to our original subroutine we were looking at, and rename that too – this seems to be something like SetupPhysXSDKLoad, so we’ll name it that.

This is a relatively small subroutine, and all it does is write the two aforementioned registry values, and that’s it. There are no other references to this subroutine beyond one early in the boot process – so at this point I’m fairly certain that Mass Effect’s executable never actually reads these values, and at this point I’m still not sure what EpicLocalDllHack does.
Cracking open PhysXLoader.dll
Now we know that Mass Effect’s executable never reads this key, it must be in one of it’s dll’s. While I won’t show it here, using ProcMon (a great tool for modding and doing things like this in general), I could see that the registry value was read right before the library was loaded in the MassEffect.exe process, and the local dll was loaded. I observed it reading the system one when I denied Mass Effect write permissions to this directory, and the game not loading at all when there was no system version of Legacy PhysX installed.
The first dll loaded is PhysXLoader, after which PhysXCore.dll loads, so that is our logical dll to analyze. Let’s crack this open in IDA and see where enableLocalPhysXCore gets used there. I’m also going to pop this dll open in Ghidra so I can get a better idea of what’s going on. Doing the same procedure as above for finding where enableLocalPhysXCore’s string is used, we find this subroutine:
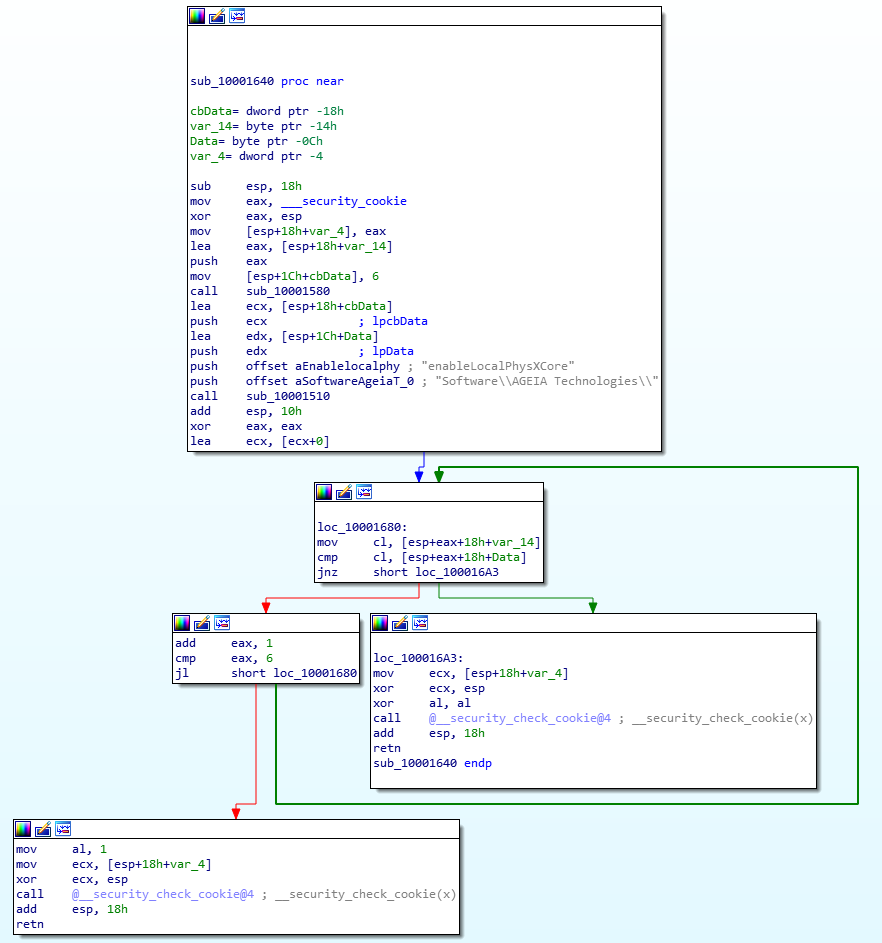
This is not too hard of a subroutine to read, especially in graph view – we can see there’s a loop from the left box going to the box above it. Still, not the easiest thing for a novice to read, so let’s see what this looks like in Ghidra. I use the location of this subroutine to jump to it in Ghidra (0x10001640).
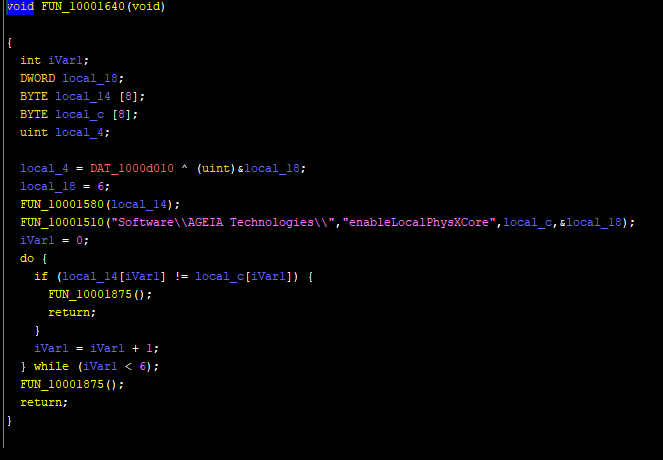
This gives us a bit more of an idea what’s going on – the subroutine calls, the loop, the return type of the subroutine. We can identify things in one tool and label them in both to help us figure out what we’re doing. Immediately we can see that there’s a subroutine call that passes a registry key path, a value name, as well as two variables. In the loop we can see it’s comparing 6 items by index to determine if they’re the same.
Just to make this a post a bit shorter, that registry lookup subroutine is indeed, a simple registry fetch wrapper. Its parameters after reverse engineering (which mostly was just mapping subroutine inputs to what they are for the windows api calls) are subkey, valuename, returned data pointer, returned data size.
You can see it has a loop that runs for 6 iterations, checking each value is identical. Using the information we’ve gained, we can rename some variables to get a better picture of what this subroutine is doing.
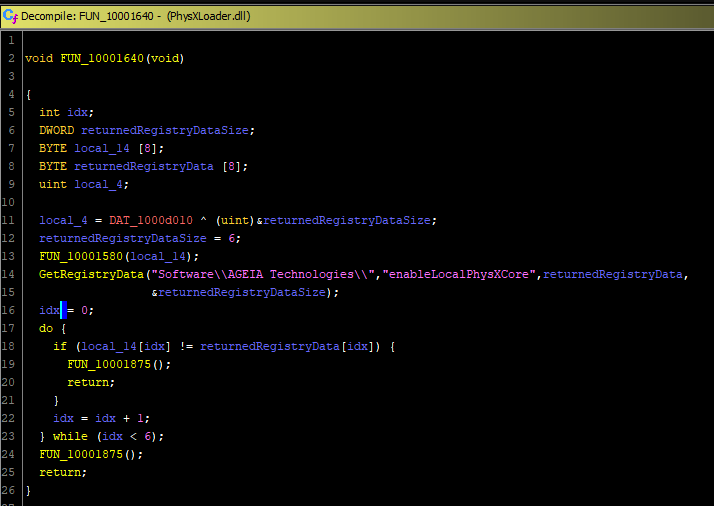
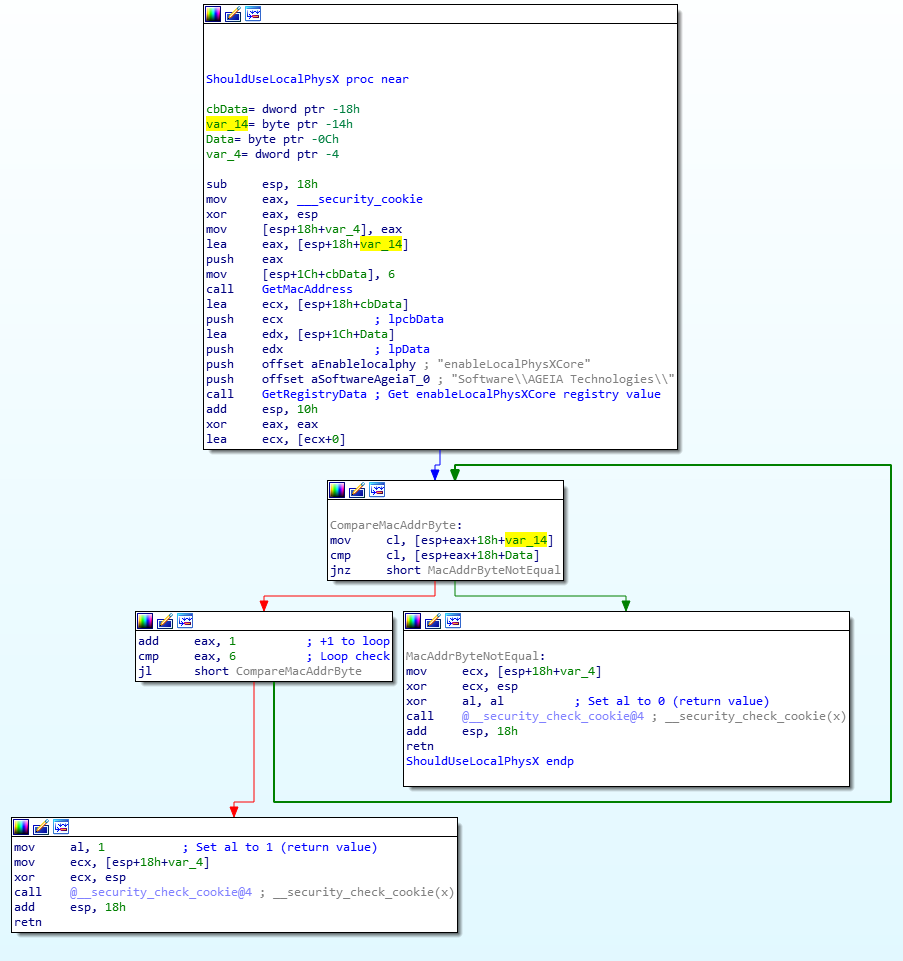
We know that Mass Effect wrote a 6 byte mac address to the registry, and that PhysXLoader.dll just read that value from the registry, and the subroutine is comparing something byte by byte 6 times. Logically, we can assume that in the above picture local_14 is the MAC address. Knowing this as well, we can guess that FUN_10001580 is fetching the MAC address and setting it, so we’ll rename some more items in this subroutine.
Now, this subroutine call seems to not do the actual loading – it is just checking for the key, and if the MAC address matches. Given the name and what we know about this key’s activity, we can give this subroutine an educated guess of a name of ‘ShouldUseLocalPhysX’. Comparing IDA and Ghidra’s decompilation of this subroutine however lead to slightly different results, with Ghidra’s seemingly being wrong:
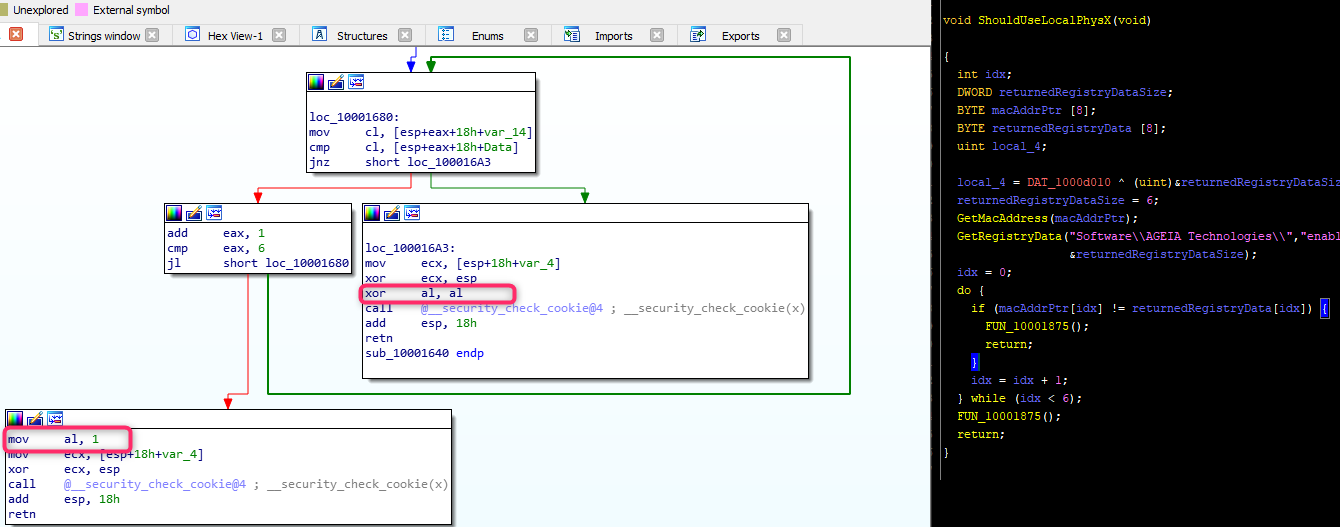
After doing some googling for this part of the post, I learned that EAX is typically used as the return register for x86, and the ‘al’ register is the bottom 8 bits of EAX. I’m not experienced enough with Ghidra to know how to retype the signature for this kind of lower 8 bits being returned, it may be just something Ghidra does not support currently, or I am missing a setting I was supposed to use.
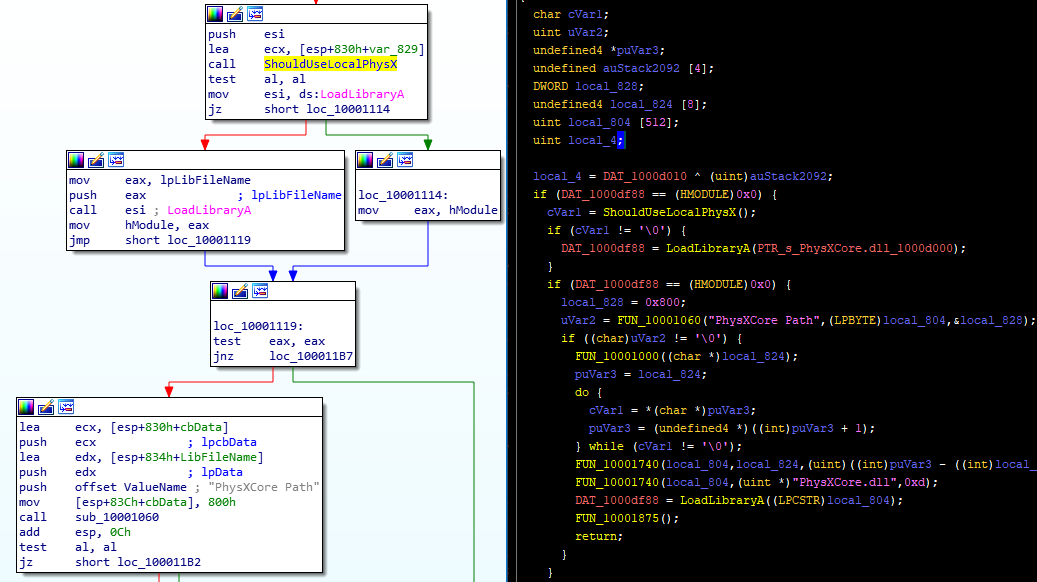
However, if we look at the references to this subroutine (there are two – likely one for each library) in IDA and Ghidra, we can see that ShouldUseLocalPhysX is being called, it’s checking if al is not zero. If it’s not zero, it loads the local PhysXCore.dll. If it is, it appears to look it up through the system PhysX installation, which is identified by another registry value in the AGEIA Technologies key named PhysXCore Path. We’re not really interested in that, since we’re looking to force PhysX to always load locally, regardless of the enableLocalPhysXCore being set or not.
Looking at the other cross reference, we can indeed see it’s loading the NxCooking library, using ShouldUseLocalPhysX in the same way:
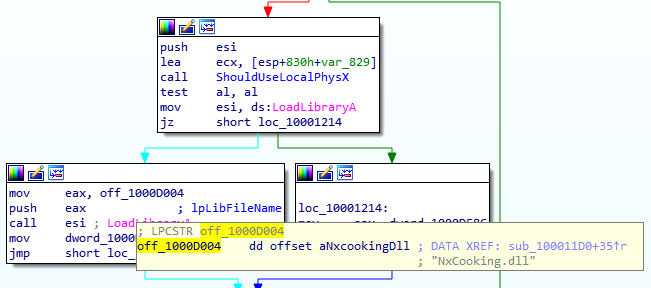
Armed with this knowledge, there are a few ways we could fix this. I’ve done a lot of function modding in UnrealScript bytecode, which for a very long time could not be extended or shrunk in size, so figuring out ways to make logic checks fail or pass without changing the size of the script was a challenge.
For example, if I needed an if check to essentially be removed, I’d need to find a way to change the comparisons to always be true or false. One way I could make an if check fail would be to modify the object references and comparison bytecode tokens to produce a condition such as if (objectA != objectA), will always produce false (assuming they are not null). We need to find a way in ShouldUseLocalPhysX here to always produce a true result.
When I was writing a symbol table for Megaman Battle Network 3, I learned to comment everything I figured out about the disassembly. I would work on something for hours, totally forgetting what I did, but could come back to my comments and understand it again.
Sometimes my symbols/comments on certain lines, such as subroutine names or pointer tables I’d identified, would come up in other subroutines, giving me useful context that I would not have seen otherwise. I’ve commented and labeled several items below, which make reading this subroutine easier.
Patching out the world’s worst boolean check
We need to ensure the bottom left block is always reached – while also making sure we don’t touch the stack (which can EASILY nuke the whole program). Technically, we could just rewrite some of this subroutine, but I’d like to make the least amount of change possible here. We need to essentially make sure the jump to the bottom right block never happens.
Conveniently, x86 has a 1 byte instruction named ‘nop’, which does literally nothing but take up one byte. Also conveniently, the jump instruction to that block is 2 bytes, comprising of a 0x75 (jnz rel8) and a 0x19 (relative offset).
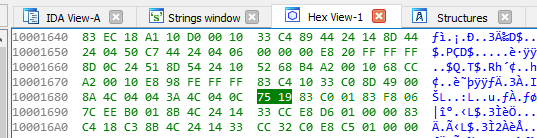
[FUN SIDE STORY] Seeing a 1-byte offset brings me back to my Megaman Battle Network modding days, where jump/branch instructions would make or break moddability for certain sections of the ROM. When writing a hook (which redirects the program counter to your own code), you had to find a jump or branch instruction, which you would modify it’s relative offset to point to your code. You would then push registers onto the stack, run your code, then put the stack back together so the subroutine exited like it should.
ARM (more specifically, THUMB) had limited branch instructions that used different sizes for their relative offsets, which were not able to always jump to any point in the ROM due to their location in the ROM. Since the game was written in assembly, finding free space at times could be difficult – sometimes you’d have to chain multiple hooks until you could get the program counter into to a free area to write new assembly code. This jnz uses opcode 0x75, which is jnz rel8, so it can only jump up to 128 bytes (or is it forward only, so 255 bytes?) away, which would be a real problem if I was doing assembly modding the way we used to back before we had fancy tools like IDA and Ghidra. [END OF FUN SIDE STORY]
Anyways, after we nop out that jnz to the not-matching block of assembly, our ShouldUseLocalPhysX subroutine now looks like this:
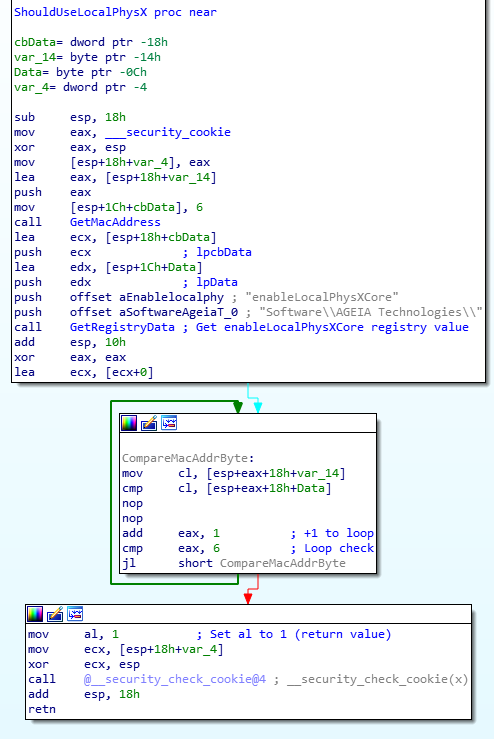
Now the not equal block cannot be reached. The ‘check’ still occurs, but it never can return false. The local PhysX core dll will always be used.
What are the downsides?
The PhysXLoader.dll file is signed by Epic Games, so this obviously breaks the signature since we modified the file. The game is not checking signatures on load, so that’s not an issue. Some antivirus programs may complain about broken signatures, but over time that typically improves. Outside of writing an in-memory patch (like we do with the asi mod loader our scene has), we would have to modify the binary of the library.
Final behavior
Using this patched dll, the game now works with or without the registry value, which means Mass Effect no longer needs administrative rights at all to run. Disassembling this was a real rant-fest because I could not get over the asinine way this check was implemented, not just a registry value but a match on MAC address too. While I was debugging and stepping through the instructions, I actually broke the game because I turned on my VPN and my MAC address it used changed.
This was a good learning experience, I’ve learned more about Ghidra and IDA, and about more problems in the PC version of Mass Effect. This patch is automatically applied as part of the install step of ALOT Installer, so users will never need to worry about having the enableLocalPhysXCore key set after it’s patched. We also modify the Mass Effect executable to write a value named enableLocalPhysXCor_, so our patched versions won’t write the value that breaks games. Vanilla Mass Effect executables will still break other games, but it is beyond the scope of our program to try and protect people’s software from poorly written PhysX loaders.
Essentially, this is how I felt afterwards:

Oh, and what about EpicLocalDllHack? Well… it does literally nothing. Absolutely worthless, it’s never read. The only thing I can think of that it could maybe exist for is to keep the registry key around if a PhysX redistributable is uninstalled, as it’s not part of the PhysX redistributable’s list of values – but that’s just a guess.
Was having a parameter ‘PreferLocalSDK’ for PhysXLoader.dll too much to ask for Epic Games?
